HSVの計算について
今回のプログラムを組むのに色相について調べていたのですが 2017年12月9日現在、WikipediaによるとRGBからHSVへ変換する際に 色相\(H\)の求め方の公式として \[ \tan H = \frac{\sqrt{3}(G-B)}{2R-G-B} \] と書いてあります。しかし、すぐにわかるように\( 2R-G-B = 0 \)の場合が定義できないことが分かります。 \( R = G = B \)といったケースで色相は元々定義できないのですが それ以外の場合で定義できないケースが発生するのは流石におかしく感じます。 どうもWikipediaの記述が不完全ではないのかという気がしましたので、自分で計算してみることにしました。 以下やや横柄な文体になります。説明はそういう文体のほうが慣れていまして…
大まかな流れを言うと色相は\( R,G,B \)の各要素から色の明るさを表す明度を差っ引いたときの比率で定義づけることができる。 その比の集合を\( \mathscr{H}\)とするとこの\( \mathscr{H}\)こそが色相の本質である(\( \mathscr{H}\)については後で正確に定義する)。 \( \mathscr{H}\)を視覚的にとらえるように六角形(または近似して円)状にして表すことが多い。 さらにその六角形から角度を対応させることにより1つの数字で色相を表現でき、 一般に色相はこの数字のことをさすことが多い。以下それを細かく述べる。
\( R = G = B \)ではないものとする。
このとき \( V = \min (R,G,B) \)として
\[ R' = R - V \\ G' = G - V \\ B' = B - V \]
としたとき\( \tilde{H} = ( R':G':B') \)とする。(当然\( R',G',B' \)のうち少なくとも1つは0である)
RBGの各色に対する\( \tilde{H}\)の集合を\( \mathscr{H}\)とする。(\(\tilde{H}\in \mathscr{H}\))
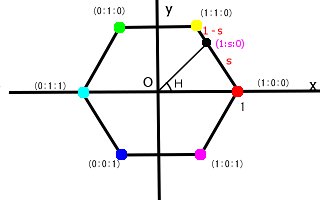
さて図のように\( ( 1:0:0) ,(1:1:0),(0:1:0),(0:1:1),(0:0:1),(1:0:1) \)を次のような正六角形の頂点に対応させる。
正六角形は単位円上にあり\( ( 1:0:0)\)を表す頂点の座標は\((1,0)\)となるようにする。
また\( X = \max (R',G',B') \)として
\[ R'' = \frac{R'}{X} \\ G'' = \frac{G'}{X} \\ B'' = \frac{B'}{X} \]
とおくと\( \tilde{H} = ( R'':G'':B'') \) であり、
\( R'',G'',B'' \)は1と0の間の数であり、\(\max (R',G',B') = 1 , \min (R',G',B') = 0\)である。
すなわち\(\tilde{H}\)は
\[( 1:s:0), \ ( 1:0:s),\ ( s:1:0),\ \\( s:0:1),\ ( 0:1:s),\ ( 0:s:1)\]
のいずれかで書ける。
ここで\(( 1:0:0), (0:1:0),(0:0:1)\)の頂点を便宜的に原色点と呼ぶことにしよう。
六角形の辺において、2つの頂点を辺の持つ原色点から\(s : 1 - s \)に内分する点に頂点の比の値を各々\(s : 1 - s \)に内分した比を対応させる。
つまり頂点\((r_1:g_1:b_1), (r_2:g_2:b_2)\)から\(s : 1 - s \)に内分する点は
\[(sr_1 +(1-s)r_2 \ , \ sg_1 +(1-s)g_2 \ , \ sb_1 +(1-s)b_2 )\]
となる。
例えば\( ( 1:0:0) ,(1:1:0)\)を\(s : 1 - s \)に内分した点は
\( (1:s:0)\)になる。
この対応により\( \mathscr{H}\)の元と六角形上の点が1対1に対応する。
そして六角形上の点は六角形の中心と\(( 1:0:0)\)の点を結ぶ線分との角度により
数値と対応させることができる。
\[ \mathscr{H} \longleftrightarrow 六角形 \longleftrightarrow \mathbb{R} / 2\pi\mathbb{Z} \]
(注:\(\mathbb{R}\)は実数全体の集合、\(\mathbb{Z}\)は整数全体の集合を表し、\( \mathbb{R} / 2\pi\mathbb{Z}\)で実数を \( 2\pi\)の整数倍したものはすべて同一視した集合を表す。
例えば\( \mathbb{R} / 2\pi\mathbb{Z}\)において \(1 = 1 + 2\pi\ = 1 + 4\pi = 1 + 2n\pi \)となる。)
まず\( R \geq G \geq B \)である場合を考えよう。 六角形でいうと\( ( 1:0:0) ,(1:1:0) \)を結ぶ辺上の点である。 この場合は\( R'' = 1 , B'' = 0\)であるから\( G'' = s\)とおくと \(\tilde{H} = (1:s:0)\)となる。 六角形を単位円に内接するものとして考え、原色点\( ( 1:0:0) \)を\( (1,0)\)の座標として考えたとき \((1:s:0)\)の座標は \[ ( 1 - \frac{s}{2} , \frac{\sqrt{3}s }{2}) \] となり、 \[ \tan H = \frac{\frac{\sqrt{3}s }{2}}{1 - \frac{s}{2}} = \frac{\sqrt{3}s }{2 - s} \] となる。ここで \( s = G'' = \frac{G'}{R'} = \frac{G - B}{R - B} \)であるから \[ \tan H = \frac{\sqrt{3}(G-B)}{2R-G-B} \] となる。
次に\( R \geq B \geq G \)である場合を考えよう。 この場合上と同じ原色点\( ( 1:0:0) \)を持つ。 上と同様に考えればよいのだが今回は回転方向が逆なのに注意すると \[ -\tan H = \frac{\sqrt{3}(B-G)}{2R-G -B} \] であるから、 \[ \tan H = \frac{\sqrt{3}(G -B)}{2R-G -B} \] となり\( R \geq G \geq B \)の場合と同じ式で表すことができる。 すなわち\( R = \max (R,G,B) \)の場合、 \[ H = \arctan (\frac{\sqrt{3}(G-B)}{2R-G-B}) \] となる。
\( G = \max (R,G,B) \)の場合や\( B = \max (R,G,B) \)の場合も
同様にできるのだが、それぞれ原色点が上の場合より\(\frac{2}{3}\pi,-\frac{2}{3}\pi\)だけ
回転させた位置にあることに注意をすると
\( G = \max (R,G,B) \)の場合は
\[ H = \arctan (\frac{\sqrt{3}(B -R)}{2G-B -R}) + \frac{2}{3}\pi\]
\( B = \max (R,G,B) \)の場合は
\[ H = \arctan (\frac{\sqrt{3}(R -G)}{2B-R -G}) - \frac{2}{3}\pi\]
となる。
まとめると次のようになる。 \[ H = \cases{ \arctan (\frac{\sqrt{3}(G-B)}{2R-G-B}) & (\(\max (R,G,B) = R\))\cr \arctan (\frac{\sqrt{3}(B -R)}{2G-B -R}) + \frac{2}{3}\pi & (\(\max (R,G,B) = G\))\cr \arctan (\frac{\sqrt{3}(R -G)}{2B-R -G}) - \frac{2}{3}\pi & (\(\max (R,G,B) = B\)) } \] で\( -\pi \leq H \leq \pi\)となる。
ここでは角度はいわゆるラジアン表記で表したが、度数表記で0から360の範囲で表したいときは上の\( H \)に対して \( \frac{360}{2\pi} H + 180\)を計算することで求めることができる。
