置換

列Xが与えられたときそれの順番を置き換えるような操作を置換という。 とくに2つの要素を入れ替えるような置換を互換といい、入れ替える要素を\(x,y\)とすると\((x\ y)\)と表す。 たとえばアルファベットの列\(\{A,B,C,D,E \}\)を\(\{C,A,E,D,B \}\)とする変換は置換である。 \(\{1,2,3,4,5,6 \}\)に互換\((2 \ 5)\)で変換すると\(\{1,5,3,4,2,6 \}\)となる。 まったく変化させない置換は恒等写像と呼ばれる。（注：恒等写像は置換に限らず、値を変化させない写像すべてに用いられる用語である）

Xにおける2つの置換を\(\rho,\sigma\)とすると、積\(\rho\sigma\)を考えることができる。 \(\rho\sigma\)は先に\(\sigma\)を行って、次に\(\rho\)をすることに注意しよう。
\[\rho\sigma : X\stackrel{\sigma}{\rightarrow}X\stackrel{\rho}{\rightarrow}X \] 例として\(\{1,2,3,4 \}\)において\((1\ 2)(1\ 3)\)を考えると
\[\{1,2,3,4 \}\stackrel{(1 \ 3)}{\rightarrow}\{3,2,1,4 \}\stackrel{(1\ 2)}{\rightarrow}\{3,1,2,4 \} \] であり、次に\((1\ 3)(1\ 2)\)を考えると \[\{1,2,3,4 \}\stackrel{(1 \ 2)}{\rightarrow}\{2,1,3,4 \}\stackrel{(1 \ 3)}{\rightarrow}\{2,3,1,4 \} \] となる。このように一般的に置換の積は可換ではない。（つまり積の順番を入れ替えたとき同じものになるとは限らない）

さて置換において次の定理が成り立つ。

定理 任意の置換は互換の積で表される。

さらにこの互換の積の表し方は一意的でない（すなわち色々な表し方がある）が
その互換の個数の偶奇は置換ごとに一意に定まる。

定理 偶数個の互換の積で表される置換は奇数個の互換の積で表すことができない。 奇数個の互換の積で表される置換は偶数個の互換の積で表すことができない。

つまり置換は互換の積で表したときに互換の数が偶数か奇数で分類できることになり
奇数個の互換の積で表される置換を奇置換、
偶数個の互換の積で表される置換を偶置換と呼ぶ。
このとき、同じ互換の積を考えるとそれは恒等写像であるから
恒等写像も偶置換になる。

応用例1　15パズル

15パズルと書いたがここでは一般のm*nのケースで考えてみよう。

先に結論を言うと、クリアとなる配置（以下、初期配置）から奇置換で配置した場合解くことができず（解が存在しない）、 偶置換で配置された場合のみ解くことができる。それを以下証明する。
便宜上、初期配置からパズルを開始する配置への置換を初期置換と呼ぶことにする。 初期配置から空マスを移動させて、空マスの初期位置に帰ってきたとする。このような置換を便宜上、空マス置換と呼ぶことにしよう。 この空マスを１つ移動させるという操作は隣接するタイルと交換するという変換、すなわち互換である。
空マスが同じ位置に戻ってきたということは空マスが上に動いた回数と下に動いた回数は等しく、右に動いた回数と左に動いた回数も等しいということになる。 すなわち動いた回数の合計は
(上に動いた回数 + 下に動いた回数 + 右に動いた回数 + 左に動いた回数) = (上に動いた回数 + 右に動いた回数)*2となり偶数である。 これにより任意の空マス置換は偶置換となる。
これにより初期配置が奇置換の場合は解くことができないことがわかる。 なぜなら、奇置換と偶置換の積は奇置換であるから（証明は明らか）、 初期値間に空マス置換を掛け合わせても奇置換であるため恒等置換にはならないからである。

さてここで注意してもらいたいのが上で奇置換の場合解けないということを示しただけである。
偶置換の場合必ず解けるかどうかはまだ示していないことになる。言葉を変えれば 偶置換による配置は解くことができるための必要条件にすぎないわけである。
そこで必ず解けることを示そう。具体的に手順を示すことで存在性を証明する。 まず \(m \ge 3 , n \ge 3\)であると仮定しよう。
このとき左端の列が初期配置と同じようにできることを示す。
まず偶置換によって配置されたタイルたちを左上から順番にタイルを移動させて詰めていく。 このとき最後のタイルは単純に移動させて敷き詰めることができないがうまく移動させることで 最後のタイルも敷き詰めることができる。
これについて考えよう。
最後から2番目のタイルをA、最後のタイルをB、空のタイルをXとする。
XをAとBでない位置を移動してもAやBは不変であることに注意しよう。
まず最後から2番目のタイルを埋めた際に最後のタイルも初期位置へ移動した場合は問題ない。 そうでない場合下図のような配置に容易にできる。

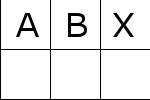
これを移動させていくことで次のようにして最後のタイルを敷き詰める。

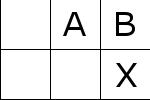
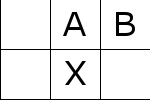
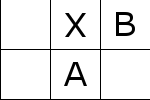
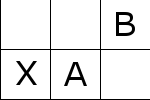
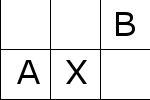
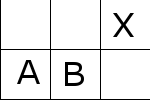
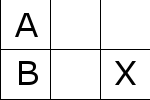
この事実より帰納法を使って、\(m = 2 , n = 2\)のケースに帰着できる。
このとき下図のように\(\{1,2,3\}\)の数列として考えよう。

偶置換による初期配置から\(m = 2 , n = 2\)のケースにまで持ってくるまでの置換Xは 空タイルの位置が右下隅で一致しているので偶置換であることに注意しよう。 つまり初期配置から考えてこの\(m = 2 , n = 2\)のケースに置き換える置換は 初期置換と置換Xの合成なのでやはり偶置換である。 よって\(\{1, 2, 3\}\)を偶置換で変換した配置となっていることが分かる。
ここで\((1\ 2\ 3)\)で1を2に2を3に3を1に置き換える置換としよう。
\((1\ 2\ 3) = (1\ 3)(1\ 2)\)であるからこの置換は偶置換である。
つまり\((1\ 2\ 3)\)を用いて\(\{1,2,3\}\)を並べ替えると、 \(\{2,3,1\}\)となる。\((1,2,3)^2\)（偶置換を2回繰り返したものは偶置換）を用いると\(\{3,1,2\}\)となる。 また\((1\ 2),(1\ 2)(1\ 2\ 3),(1\ 2)(1\ 2\ 3)^2\)は奇置換であるから、これを用いた配置は \(\{2,1,3\},\{1,3,2\},\{3,2,1\}\)である。 3つの数の並べ方は6通りであるから、これらで全てである。 このように偶置換による配置は\(\{1,2,3\}),\{2,3,1\},\{3,1,2\}\)の3つとなるが、 これらは空マスを右回りに1周させる操作は\((1\ 2\ 3)\)であるから、 \(\{1,2,3\}),\{2,3,1\},\{3,1,2\}\)はいずれも\(\{1,2,3\}\)にすることができる。

応用例2

図のように三角形上に数を並べた配置を考える。
(図１)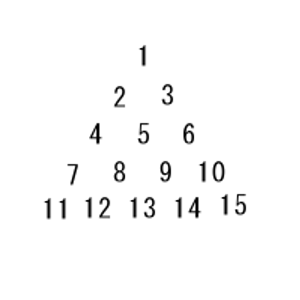
これに対して任意の場所で3つの数だけが入る小さな三角形の領域を考えて、 その領域内にある数を右回りに巡回させる変換を考える。
例えば下の図2のように2,4,5を含む領域を選んだとき
(図2)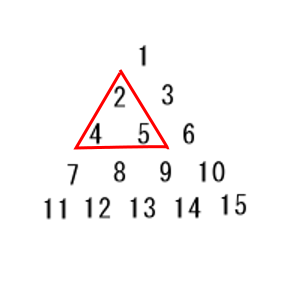
右回りに巡回させると図3のようになる。
(図3)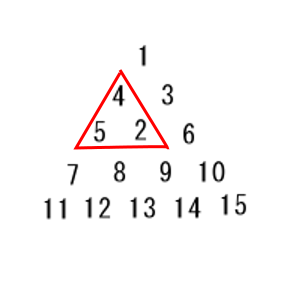
さてこのような変換たちにより 任意の三角形上の配置を置き換えて図１の状態に持っていけるだろうか。 結論を先に言うと否である。 なぜなら、三角形の内部にある数を\(a,b,c\)とするとこれらを巡回させる変換は 例1での表記に従えば\((a\ b\ c)\)であり、これは\((a\ c)(a \ b)\)でもある。 つまり三角形内で巡回させる変換はすべて偶置換であるため、これらの積も 偶置換である。 つまり図１の状態を奇置換によって変換した配置は例１と同様にできないことが示される。

逆に偶置換の場合は必ず解くことができることを示そう。 三角形状の配置の下の段から詰めていくことを考える。三角形の段の数をdとする。
(図2-1)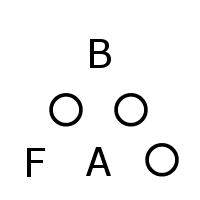
\(d\ge 3\)のとき図2-1のように下の段を左からAまでつめている状態で残りのマスをBで詰めることを考える。 まずBの位置は図2-1の位置とする（それ以外の場合でも三角形を巡回させることで持ってこれる）。 すると次の図のようにしてBを残りのマスに詰めることができる。

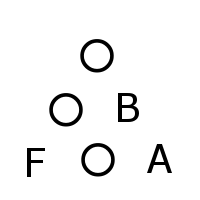
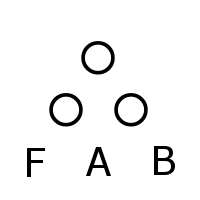
これにより\(d\ge 3\)のとき下の段から順番に詰めていくことができ、 \(d=2\)の場合を考えればよいことになる。 \(d=2\)のとき\(\{1,2,3\}\)の並べ替えになるが、これは例1の場合と同様に考えることで \(\{1,2,3\}\)にすることができることが分かる。

応用例3

1からnまでの数をランダムに並べた数列を考える。
このとき、2つの連続した数を取り出しその順序を変えないまま先頭に持ってくるという繰り返すことで この数列を\(1,2,3,\cdots,n\)とできるかどうかを考える。 例えばn = 5として、\(1,2,5,3,4\)を考えると、 連続した\(3,4\)を取り出し、先頭に持っていくと\(3,4,1,2,5\)
次に\(1,2\)を取り出し、先頭に持っていくと\(1,2,3,4,5\)とすることができる。
結論から先に言うと、\(1,2,3,4,5\)を奇置換で変換した配置の場合は\(1,2,3,\cdots,n\)とすることはできない。 今までの例とほぼ同様の考え方だが、2つの連続した数を取り出しその順序を変えないまま先頭に持ってくるという操作が偶置換であるからである。
2つの連続した数を取り出し先頭に持ってくるという操作が偶置換であることを示そう。
\(a,b,c\)を\(b,c,a\)とする置換は\((a\ c)(a\ b)\)であり偶置換。 またこれは2つの連続する数を１つ前にずらすという操作であるから、これを繰り返すことで 2つのつの連続する数を先頭にもってくることができ、これは2つの連続した数を取り出し先頭に持ってくる操作と一致する。 すなわち2つの連続した数を取り出し先頭に持ってくる操作は偶置換である。 これにより例1と同様に考えて、偶置換による配置でないと解けないことがわかる。

次に偶置換による配置なら\(1,2,3,\cdots,n\)とできることを示そう。 まず\(n\ge 3\)のとき偶置換による初期配置においてnが末尾にないときnを末尾に持っていくことを考える。
nが先頭にある場合はnの後ろの2つの数を取り出すことでnを先頭でないようにできる。 この操作を行ったときnが末尾になれば求めていた操作であり、ここではそうでない場合を考える。 そのときnが先頭でも末尾でもない状態となる。 nが奇数のとき、\(n , x\)（xはnの後ろの数）を取り出して先頭に持ってくると、nの後ろは偶数個となる。 nが偶数のとき、\(x, n\)（xはnの前の数）を取り出して先頭に持ってくると、nの後ろは偶数個となる。 nの後ろに偶数個の数がある場合、2つずつ前に持っていくことでnを末尾に持っていくことができる。 このように\(n\ge 3\)の場合はnを末尾に持っていくことができる。 これから末尾から順に数を埋めていくことができ、最後に2つの数が残るが、 ここまで行ってきた操作がすべて偶置換であるため、2つの数における偶置換は恒等写像であるため 残った数の列は\(1,2\)となる。 これにより偶置換による配置なら\(1,2,3,\cdots,n\)とできることが示された。